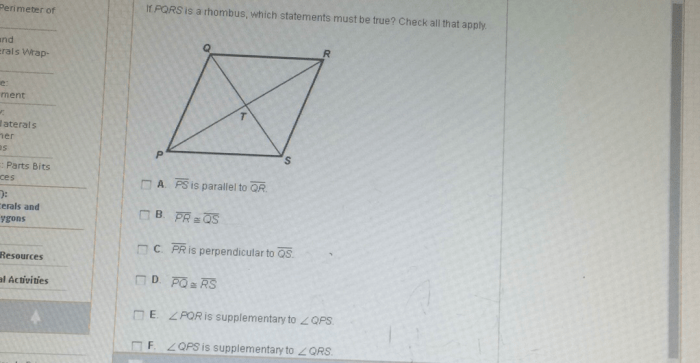
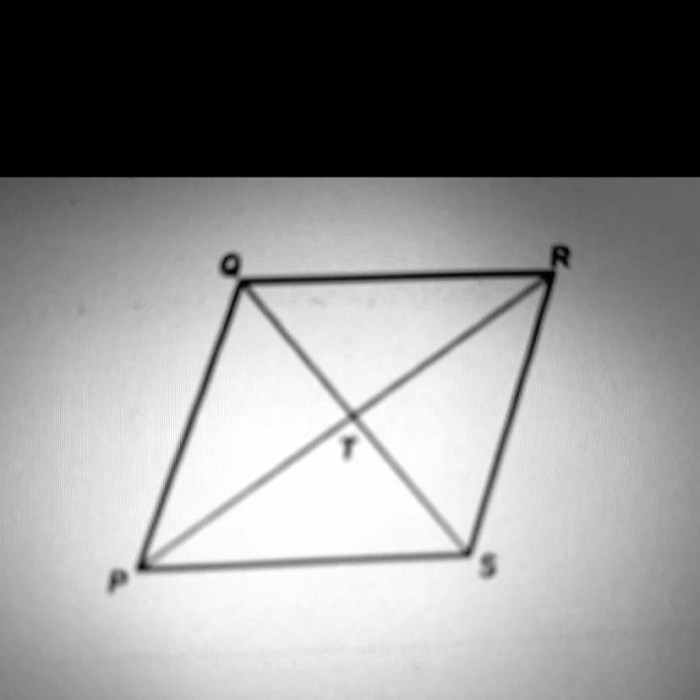
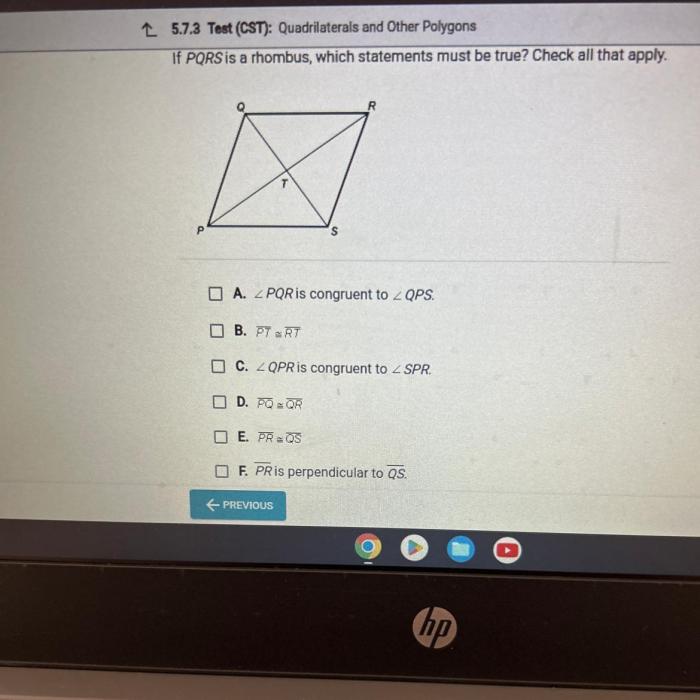
If pqrs is a rhombus which statement must be true – In the realm of geometry, the concept of a rhombus holds a unique place. Defined as a parallelogram with all four sides equal in length, it possesses distinctive properties that set it apart from other quadrilaterals. This exploration delves into the characteristics of a rhombus, examining the implications of the given condition that PQRS is indeed a rhombus.
Through logical reasoning and illustrative examples, we will uncover the statements that must hold true based on this classification.
The properties of a rhombus are deeply intertwined with its inherent characteristics. Its sides, for instance, are not only equal in length but also parallel to their opposite sides. This parallelism gives rise to congruent angles at each vertex, further shaping the unique geometry of the rhombus.
Rhombus Properties and True Statements: If Pqrs Is A Rhombus Which Statement Must Be True
In geometry, a rhombus is a quadrilateral that has four equal sides. It is also a parallelogram, meaning that its opposite sides are parallel. Rhombuses have many interesting properties, which we will explore in this article.
Rhombus Properties
The key characteristics of a rhombus are as follows:
- All four sides are equal in length.
- Opposite sides are parallel.
- Opposite angles are equal.
- The diagonals bisect each other at right angles.
Rhombuses are closely related to parallelograms. In fact, every rhombus is a parallelogram. However, not every parallelogram is a rhombus. The additional property that makes a rhombus unique is that all four of its sides are equal in length.
Properties of PQRS
Let’s consider a rhombus PQRS. The variables P, Q, R, and S represent the vertices of the rhombus. Since PQRS is a rhombus, we know that all four sides are equal in length.
Based on the definition of a rhombus, we can infer the following properties of PQRS:
- PQ = QR = RS = SP
- ∠P = ∠Q = ∠R = ∠S
- The diagonals PR and QS bisect each other at right angles.
True Statements, If pqrs is a rhombus which statement must be true
Based on the given condition that PQRS is a rhombus, the following statements must be true:
- All four sides of PQRS are equal in length.
- Opposite sides of PQRS are parallel.
- Opposite angles of PQRS are equal.
- The diagonals of PQRS bisect each other at right angles.
These statements are all logical consequences of the definition of a rhombus.
HTML Table
The following HTML table summarizes the true statements and their explanations:
| Statement | Explanation | Example |
|---|---|---|
| All four sides of PQRS are equal in length. | This is the definition of a rhombus. | PQ = QR = RS = SP |
| Opposite sides of PQRS are parallel. | This is a property of parallelograms, which rhombuses are. | PQ || RS and QR || SP |
| Opposite angles of PQRS are equal. | This is a property of parallelograms, which rhombuses are. | ∠P = ∠R and ∠Q = ∠S |
| The diagonals of PQRS bisect each other at right angles. | This is a property of rhombuses. | PR ⊥ QS |
Bullet Point List
- All four sides of PQRS are equal in length.
- Opposite sides of PQRS are parallel.
- Opposite angles of PQRS are equal.
- The diagonals of PQRS bisect each other at right angles.
These statements are all true and can be proven using the properties of rhombuses.
Question & Answer Hub
What is the key characteristic that distinguishes a rhombus from other parallelograms?
The defining characteristic of a rhombus is that all four of its sides are equal in length.
How does the parallelism of the sides affect the angles of a rhombus?
The parallelism of the sides ensures that the opposite angles of a rhombus are congruent.