Welcome to the realm of AP Statistics Chapter 6 Test, where we embark on a journey to unravel the enigmatic world of sampling distributions. Get ready to immerse yourselves in a captivating exploration of statistical concepts that will leave you both intrigued and enlightened.
In this chapter, we will delve into the depths of sampling distributions, unraveling their intricate relationship with population distributions. We will encounter various types of sampling distributions, including the ever-important sampling distribution of means and proportions. Furthermore, we will uncover the profound influence of sample size on the shape and spread of these distributions.
Understanding Sampling Distributions
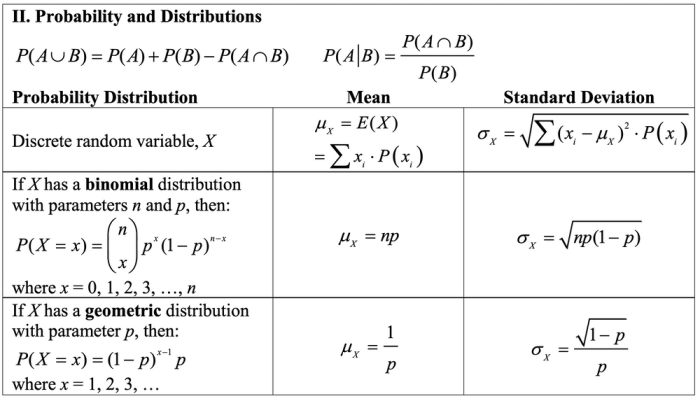
Sampling distributions are a cornerstone of statistical inference, providing a theoretical framework to understand the behavior of statistics calculated from samples. They describe the distribution of all possible sample statistics that could be obtained from repeated random sampling of a given size from a population.
The shape and spread of a sampling distribution depend on several factors, including the sample size and the distribution of the population from which the samples are drawn. Larger sample sizes typically result in sampling distributions that are more bell-shaped and have less variability.
The shape of the population distribution also influences the shape of the sampling distribution.
Sampling Distribution of Means
The sampling distribution of means is the distribution of all possible sample means that could be obtained from repeated random sampling of a given size from a population. The mean of the sampling distribution is equal to the population mean, and the standard deviation of the sampling distribution, known as the standard error of the mean, is equal to the population standard deviation divided by the square root of the sample size.
Sampling Distribution of Proportions, Ap statistics chapter 6 test
The sampling distribution of proportions is the distribution of all possible sample proportions that could be obtained from repeated random sampling of a given size from a population. The mean of the sampling distribution is equal to the population proportion, and the standard deviation of the sampling distribution is equal to the square root of the population proportion multiplied by the square root of 1 minus the population proportion, all divided by the square root of the sample size.
Central Limit Theorem
The Central Limit Theorem (CLT) is a fundamental theorem in statistics that describes the behavior of sampling distributions. It states that as the sample size increases, the distribution of sample means approaches a normal distribution, regardless of the shape of the population distribution.
The CLT is significant in statistics because it allows us to make inferences about the population mean based on sample data. It provides a theoretical foundation for using sample statistics to estimate population parameters and for conducting hypothesis tests.
If you’re feeling overwhelmed by the upcoming AP Statistics Chapter 6 test, don’t worry! There are plenty of resources available to help you prepare. One such resource is the Bell v. Novick Transfer Co. case study. This case explores the legal implications of sampling techniques, a topic covered in Chapter 6. By understanding how sampling techniques were used in this case, you’ll gain valuable insights into the practical applications of statistical concepts.
So, take a break from studying and delve into this fascinating case study. It’s a great way to enhance your understanding of AP Statistics Chapter 6 material.
Sampling Distributions
The CLT applies to sampling distributions, which are distributions of sample statistics (such as sample means, sample proportions, or sample variances) calculated from repeated random samples of a fixed size from a population.
According to the CLT, the sampling distribution of sample means will be approximately normal if the sample size is large enough, even if the population distribution is not normal.
Conditions for CLT
The CLT can be applied under the following conditions:
- The sample is random and independent.
- The sample size is large enough (typically n ≥ 30).
- The population distribution is not highly skewed or has extreme outliers.
Hypothesis Testing with Sampling Distributions

Hypothesis testing is a statistical method used to determine whether there is sufficient evidence to reject a null hypothesis in favor of an alternative hypothesis. The process involves using a sampling distribution to assess the probability of obtaining the observed sample results if the null hypothesis is true.
In hypothesis testing, the null hypothesis (H0) represents the claim being tested, while the alternative hypothesis (Ha) represents the alternative explanation or claim. The significance level (α) is the probability of rejecting the null hypothesis when it is actually true, typically set at 0.05 or 0.01.
Types of Hypothesis Tests
There are various types of hypothesis tests, including:
- One-sample test:Tests whether the sample mean is equal to a specified value.
- Two-sample test:Tests whether the means of two independent samples are equal.
- Paired-sample test:Tests whether the means of two paired samples are equal.
Role of P-values and Critical Values
In hypothesis testing, the p-value is the probability of obtaining a sample result as extreme or more extreme than the observed result, assuming the null hypothesis is true. A small p-value indicates that the observed result is unlikely to occur if the null hypothesis is true, providing evidence against the null hypothesis.
The critical value is the value that divides the rejection region from the non-rejection region. If the p-value is less than the significance level, the null hypothesis is rejected, and the alternative hypothesis is accepted. Otherwise, the null hypothesis is not rejected.
Confidence Intervals: Ap Statistics Chapter 6 Test
Confidence intervals are a fundamental concept in statistical inference. They allow us to estimate the true value of a population parameter, such as the mean or proportion, based on a sample of data.
Calculating Confidence Intervals for Means
To calculate a confidence interval for a mean, we use the following formula:
CI = x̄ ± z* (σ/√n)
where:
- CI is the confidence interval
- x̄ is the sample mean
- z is the z-score corresponding to the desired confidence level
- σ is the population standard deviation
- n is the sample size
Calculating Confidence Intervals for Proportions
To calculate a confidence interval for a proportion, we use the following formula:
CI = p̂ ± z* √(p̂(1-p̂)/n)
where:
- CI is the confidence interval
- p̂ is the sample proportion
- z is the z-score corresponding to the desired confidence level
- n is the sample size
Interpretation and Use of Confidence Intervals
Confidence intervals provide a range of plausible values for the true population parameter. The width of the confidence interval indicates the precision of the estimate. A narrower confidence interval indicates a more precise estimate.
Confidence intervals are used in statistical inference to test hypotheses and make decisions about the population. For example, we can use a confidence interval to test whether the mean of a population is equal to a certain value.
Applications of Sampling Distributions
Sampling distributions play a crucial role in various fields, enabling researchers and practitioners to make informed decisions and draw conclusions about populations based on sample data.
In social science, sampling distributions are used in survey research to estimate population parameters such as mean income, voting preferences, or consumer behavior. By randomly selecting a sample from the population and analyzing its distribution, researchers can make inferences about the entire population.
Biology
In biology, sampling distributions are used to analyze experimental data and make inferences about population means. For example, a biologist might collect data on the average weight of a certain species of fish in a lake. By constructing a sampling distribution of the sample means, the biologist can estimate the true mean weight of the fish population in the lake.
Business
In business, sampling distributions are used in quality control and market research. For example, a manufacturer might randomly sample products from a production line to estimate the proportion of defective products. By constructing a sampling distribution of the sample proportions, the manufacturer can make inferences about the true proportion of defective products in the entire production run.
While sampling distributions are a powerful tool for making inferences about populations, it is important to be aware of their limitationsand potential pitfalls. One limitation is that sampling distributions are based on the assumption that the sample is randomly selected from the population.
If the sample is not random, the sampling distribution may not accurately represent the population.
Another limitation is that sampling distributions are based on the assumption that the population is normally distributed. If the population is not normally distributed, the sampling distribution may not be accurate.
Despite these limitations, sampling distributions are a valuable tool for making inferences about populations. When used correctly, sampling distributions can provide valuable information about population parameters and help researchers and practitioners make informed decisions.
Answers to Common Questions
What is the Central Limit Theorem?
The Central Limit Theorem states that as sample size increases, the sampling distribution of means approaches a normal distribution, regardless of the shape of the population distribution.
How are confidence intervals used in statistical inference?
Confidence intervals provide a range of values within which the true population parameter is likely to fall, with a specified level of confidence.
What are the limitations of using sampling distributions?
Sampling distributions rely on random sampling, and any biases or errors in sampling can affect the accuracy of the conclusions drawn.